October 23, 2022

The (not so) secret mechanisms behind classical thin lens IOL formulas

Third generation formulas are based on thin lens optics. They have the same "skeleton". The value they use to determine the corneal power from the anterior radius of curvature differ - neither do they use the same keratometric index,  nor the same rules to predict the lens position from the biometric parameters. However, once those values are calculated, the prediction process is the same for every formula.

Let's dive into the details :-)

The SRK/T Formula

Published in 1990 by Sanders, Retzlaff and Kraff, the SRK/T (1,2) has long been the favourite IOL calculation method among ophthalmologists, and is still extremely popular.

The SRK/T formula is clever and complex. The retinal thickness (RETHICK) value depends on the AL value. AL + RETHICK gives LOPT (Optical AL), the AL value used in the optical equation. Corneal width (Cw) is a function of K and a modified AL value (LCOR). Cw and R are used to calculate the parameter H. ACD const is a transformation of the A constant value : ACD const + H - 3.336 give the lens position value. K is used natively in the optical equation, using a keratometric value of 1.333. Figure from : Debellemanière G, Dubois M, Gauvin M, Wallerstein A, Brenner LF, Rampat R, Saad A, Gatinel D. The PEARL-DGS Formula: The Development of an Open-source Machine Learning-based Thick IOL Calculation Formula. Am J Ophthalmol. 2021 Dec;232:58-69.

In this formula, the axial length is slightly modified before being used to predict the lens position. It allows to lower its impact on lens position prediction for high AL values.

def setLCOR(LA): 
	if LA <= 24.2: 
    	LCOR = LA 
    else: 
    	LCOR = -3.446 + (1.715 * LA) - (0.0237* (LA**2))
    return LCOR

To be more precise, the modified AL value (LCOR) is used, with the K value, to predict the Corneal Width (Cw). Cw and R are then used to calculate H, which is added to the transformed A constant to give the ELP.  

Cw = -5.40948 + (0.58412 * LCOR) + (0.098 * K)
def setH(r, Cw):
    x = r**2 - (Cw**2 / 4.0) 
    if x < 0: 
    	x = 0 
    else: 
    	pass 
    H = r - math.sqrt(x) 
    return H

The influence of the AL value on lens position has a ceiling...

From : Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg. 1990 May;16(3):333-40. Using a quadratic function (polynomial of degree 2) to determine the lens position from the AL, avoids the hard cut-off of the Holladay 1 formula.

... and the predACD value has a strange relationship with the anterior corneal radius value :

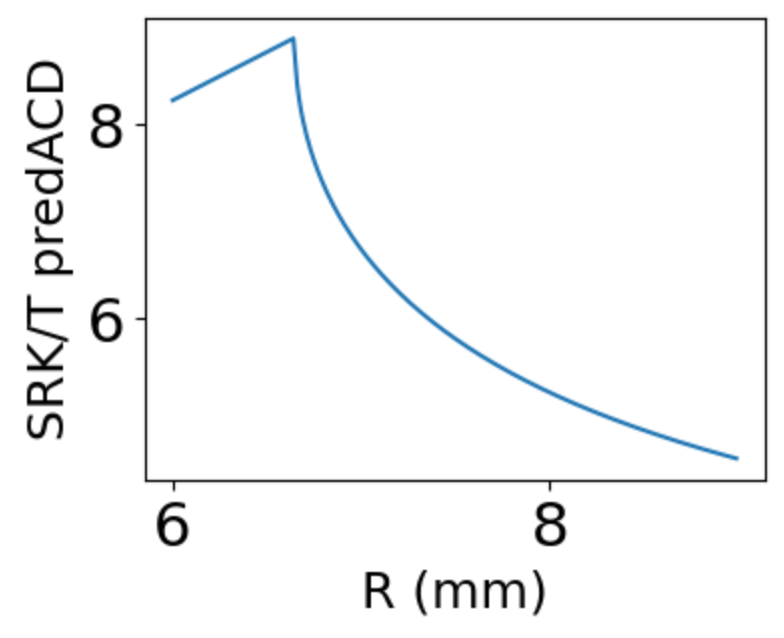
SRK/T PredACD value as a function of anterior corneal radius (AL = 23.5mm, A const. 119.0)

This is because the value entered in the square root of the formula allowing the calculation of H is set to zero when negative (3) !

Let's use a 3D representation :

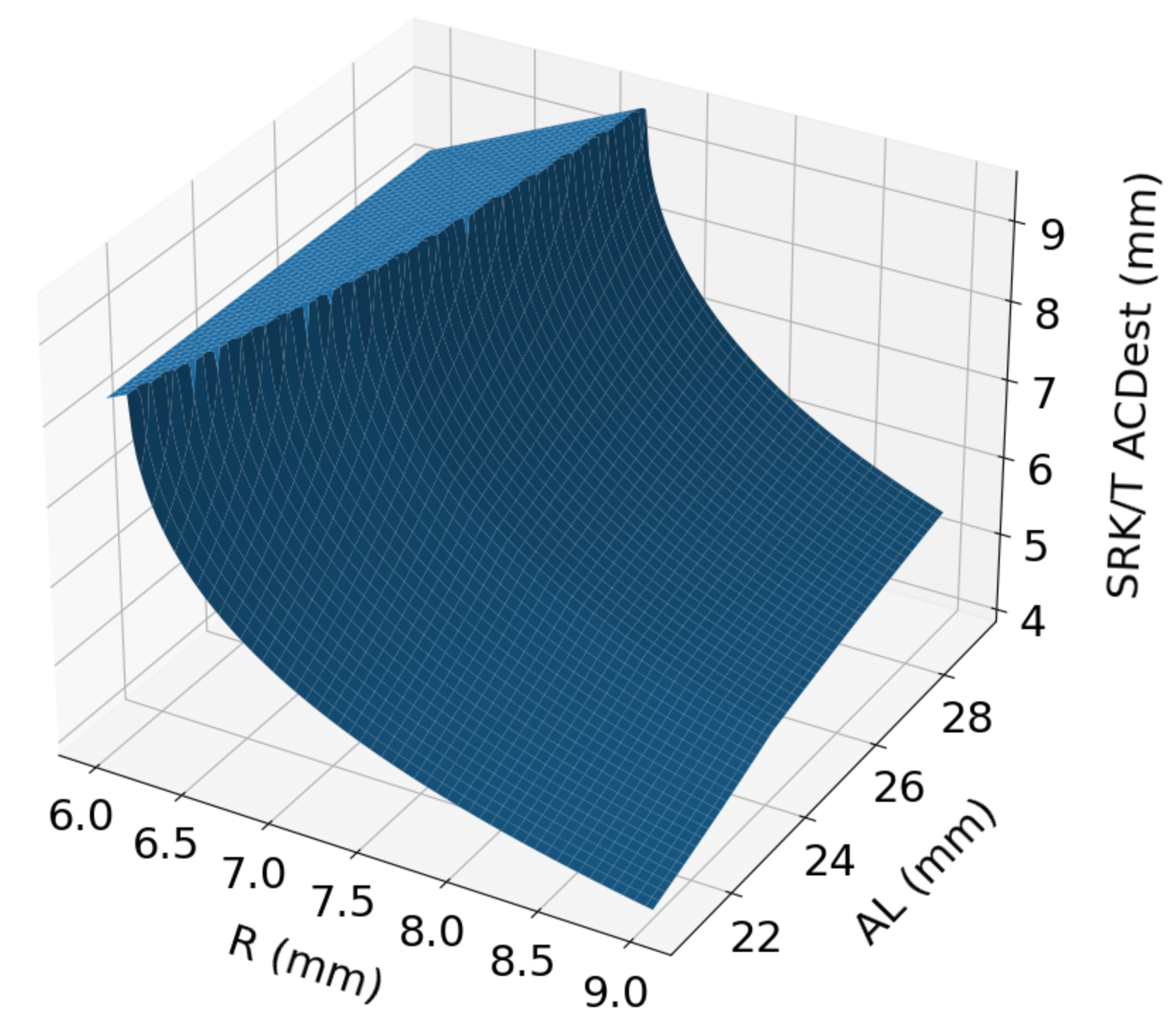
Also, note that the AL value used in the optical equation is modified by adding a theoretical Retinal Thickness (RETHICK) value to it. RETHICK is itself a function of AL. 

RETHICK = 0.65696 - 0.02029*LA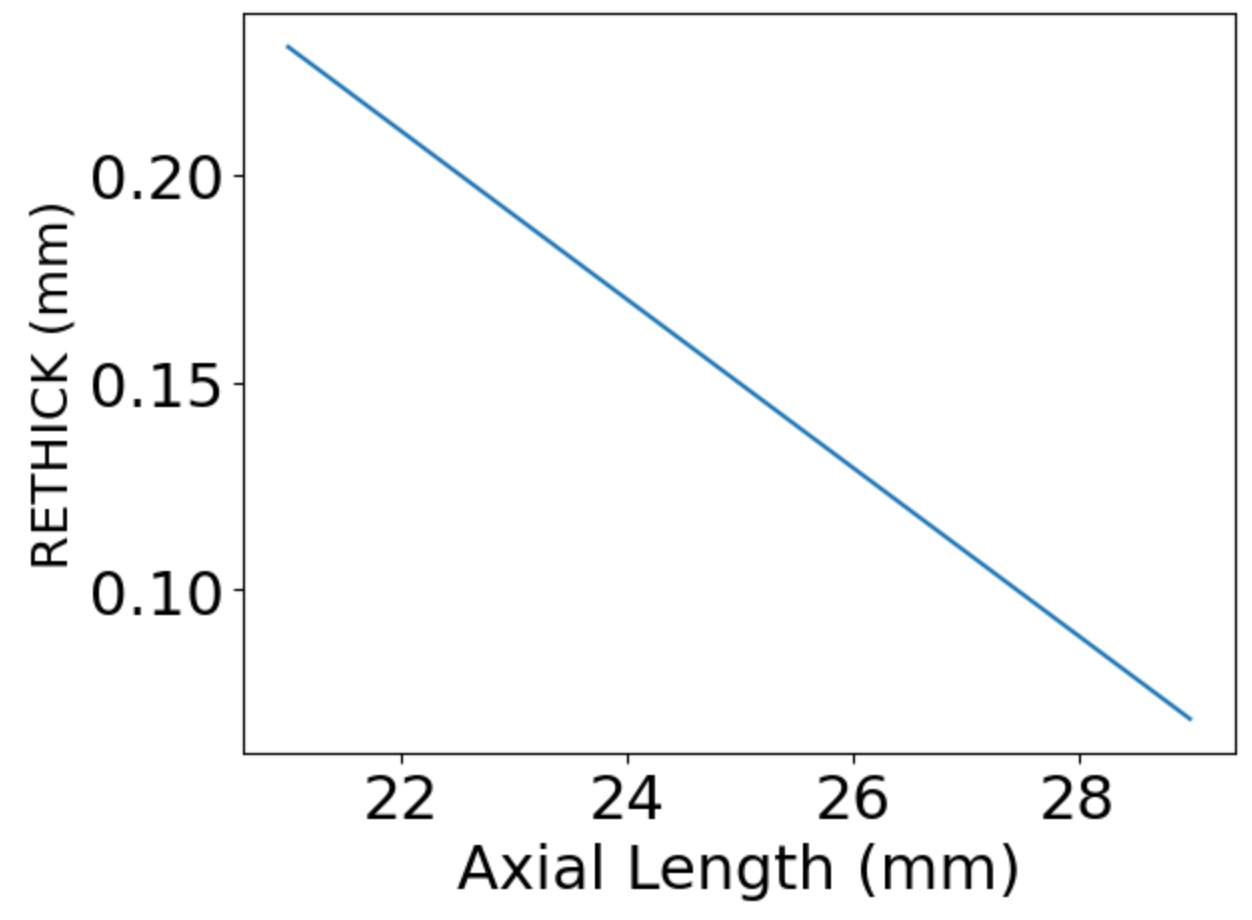
The longer the eye, the thinner the RETHICK value of the SRK/T formula.

This is the final SRK/T function : 

def SRKT_SE(LA, r, aconst, power):
    # a keratometric index value of 1.3375 is used to compute the ACD via the Cw value
    # but : a keratometric index value of 1.333 is used as the real keratometric index in the optical calculation ! (cf ncml value)
    K = 337.5/r 
    V = 12.0 
    na = 1.336 
    nc = 1.333 
    ncml = 0.333
    # the SRK A constant is modified to represent a physical offset
    ACDconst = 0.62467 * aconst - 68.747 
    offset = ACDconst - 3.336
    # The eye-specific lens position is calculated
    LCOR = setLCOR(LA) 
    Cw = -5.40948 + (0.58412 * LCOR) + (0.098 * K) 
    H = setH(r, Cw) 
    # The ELP is added to the modified A constant
    ACDest = H + offset 
    # The optical AL is equal to AL + retinal thickness
    RETHICK = 0.65696 - 0.02029*LA 
    LOPT = LA + RETHICK 
    # the thin lens calculation is finally done
    num = 1000 * na * (na *r - ncml * LOPT)- power * (LOPT-ACDest) * (na * r - ncml * ACDest) 
    denum = na * (V*(na * r - ncml * LOPT) + LOPT * r) - 0.001 * power * (LOPT-ACDest) * (V * (na * r - ncml * ACDest) + ACDest * r) 
    SEpred = num/denum 
    return round(SEpred,3)

The Hoffer Q Formula

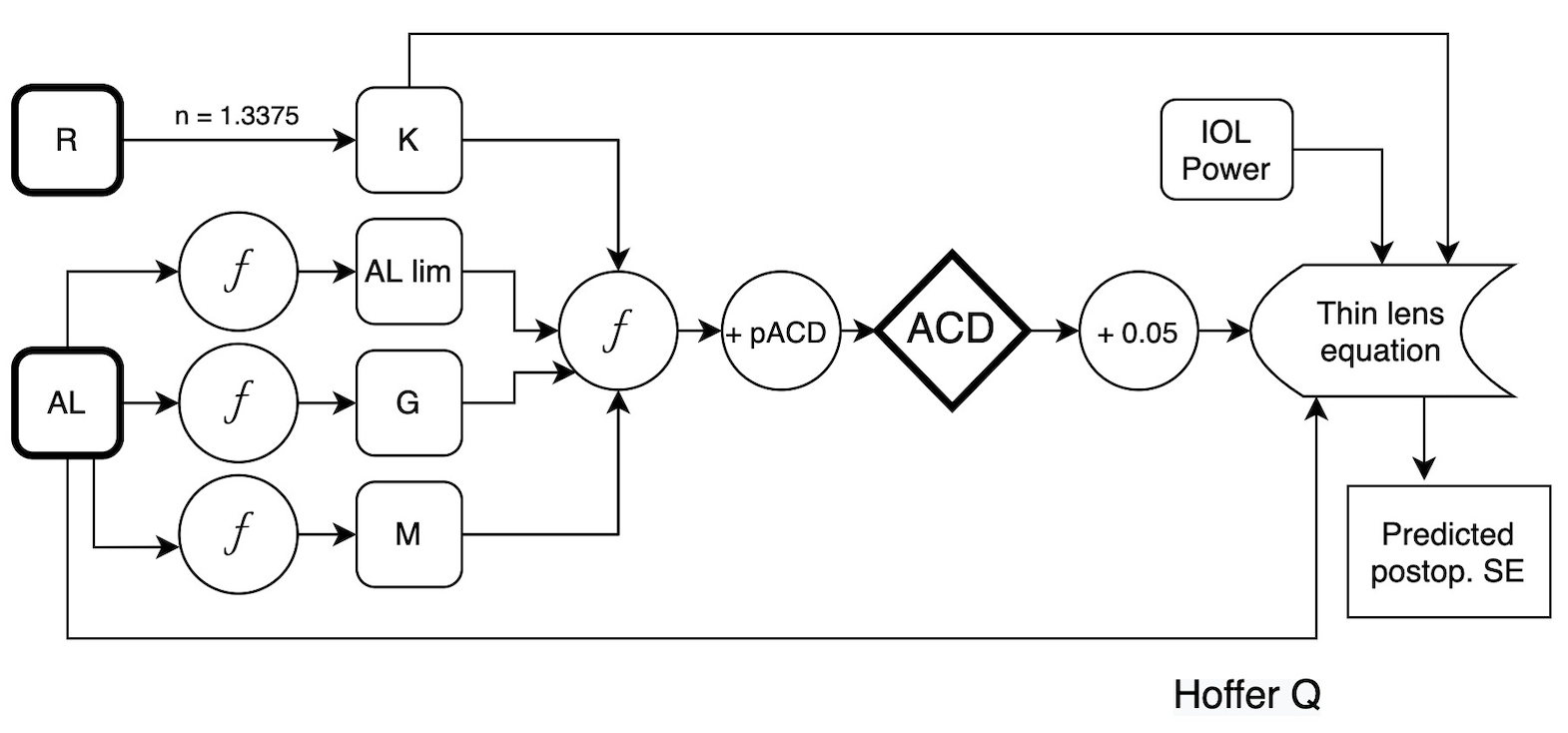
Figure from : Debellemanière G, Dubois M, Gauvin M, Wallerstein A, Brenner LF, Rampat R, Saad A, Gatinel D. The PEARL-DGS Formula: The Development of an Open-source Machine Learning-based Thick IOL Calculation Formula. Am J Ophthalmol. 2021 Dec;232:58-69.

The Hoffer Q formula (4-7) is the most difficult, among the third generations formulas, to code correctly. The AL value is used to generate 3 other values, which are used along with the K value to calculate the lens position. pACD + 0.05 is added to the predicted value. K is calculated using a keratometric index of 1.3375. The original K and AL values are used in the optical equations.

def defMG(LA): 
    if LA <= 23.0: 
    	M = 1.0 
        G = 28.0 
    else: 
    	M = -1.0 
        G = 23.5 
        return M, G
def defA(LA): 
    if LA > 31.0: 
    	A = 31.0 
    elif LA < 18.5: 
    	A = 18.5 
    else: 
    	A = LA 
    return A

The lens position function is complicated : 

import math 
def predACD(LA, K, pACD): 
    M, G = defMG(LA) 
    A = defA(LA) 
    p2 = 0.3 * (A - 23.5) 
    p3 = (math.tan(K*(math.pi / 180.0)))**2 
    p4 = 0.1 * M * ((23.5 - A)**2) 
    p5 = math.tan((0.1 * (G - A)**2) * (math.pi / 180.0)) 
    ACD = pACD + p2 + p3 + (p4 * p5) - 0.99166 
    return ACD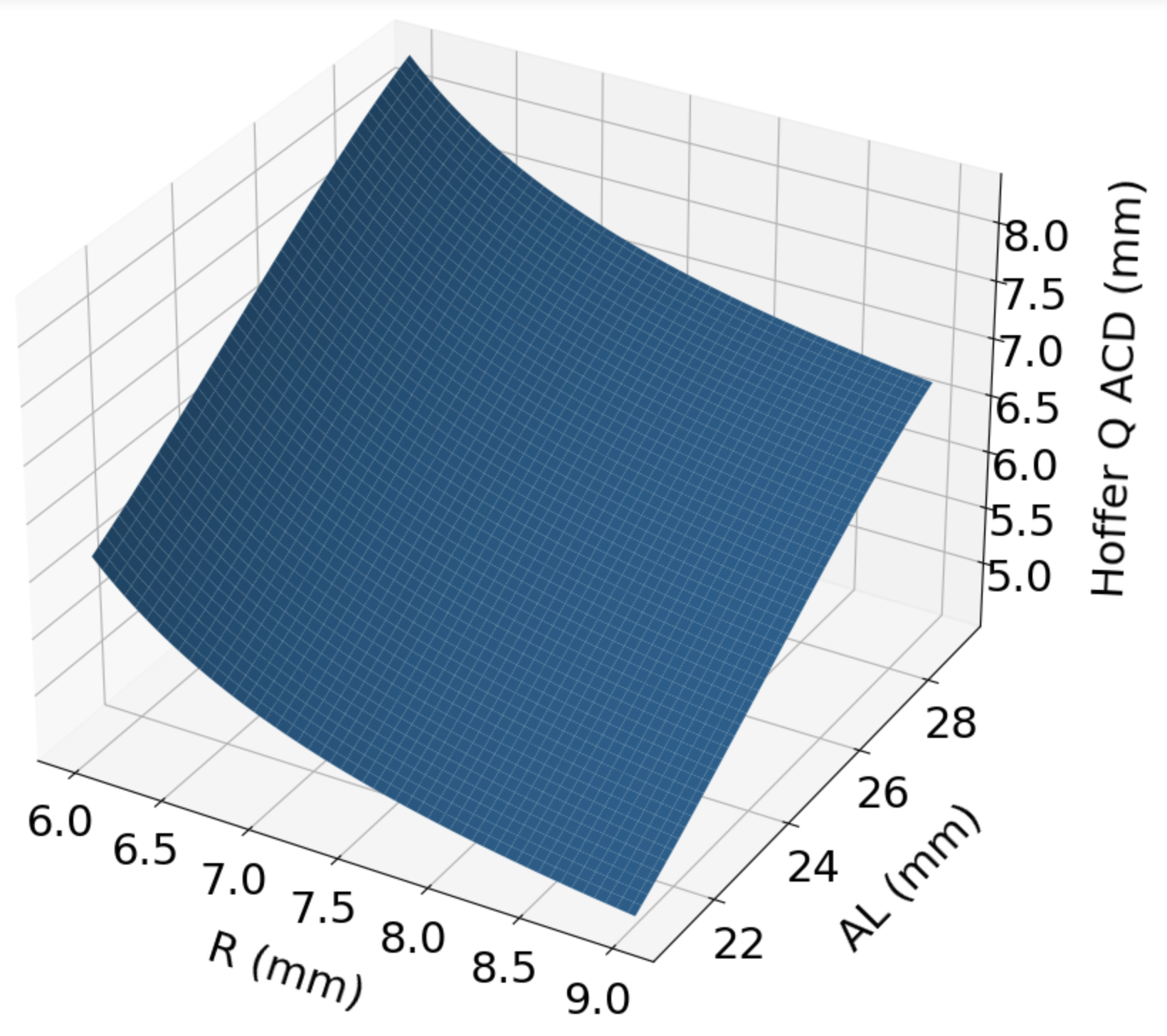

Final Hoffer Q function : 

def HofferQ_SE(LA, r, pACD, power): 
    K = 337.5/r 
    ACD = predACD(LA, K, pACD) 
    R = (1.336 / (1.336/(1336 / (LA - ACD - 0.05) - power) + (ACD + 0.05) / 1000.0)) - K 
    SEpred = R / (1.0 + 0.012 * R) 
    return round(SEpred, 3)

The Holladay 1 Formula

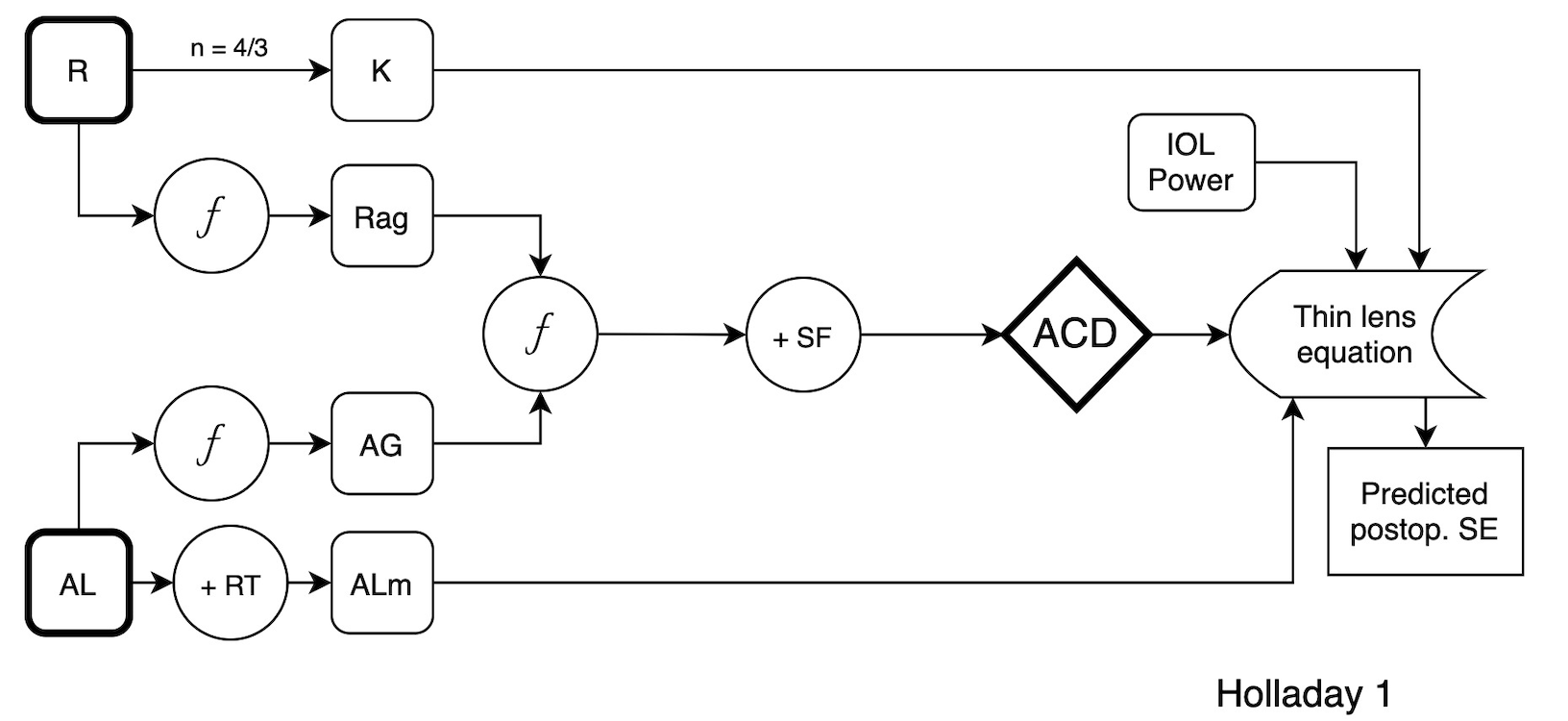
The Holladay 1 formula. The AL and R are transformed, then those transformed values are used to predict the lens position. The SF is added to the predicted value. The "original" R is used in the optical equations, using a keratometric index equal to 4/3 (1.333333.....). Retinal thickness is added to the AL value before being entered in the optical equation. Figure from : Debellemanière G, Dubois M, Gauvin M, Wallerstein A, Brenner LF, Rampat R, Saad A, Gatinel D. The PEARL-DGS Formula: The Development of an Open-source Machine Learning-based Thick IOL Calculation Formula. Am J Ophthalmol. 2021 Dec;232:58-69.

The Holladay 1 formula (8) uses a keratometric index of 4/3. The lens position (ACD) is inferred from the ARC (with a flooring below 7.0mm) and from the AL (with a ceiling after  25.32mm, approximately).

def setRag(R): 
    if R < 7: 
    	Rag = 7 
    else: 
    	Rag = R 
    return Rag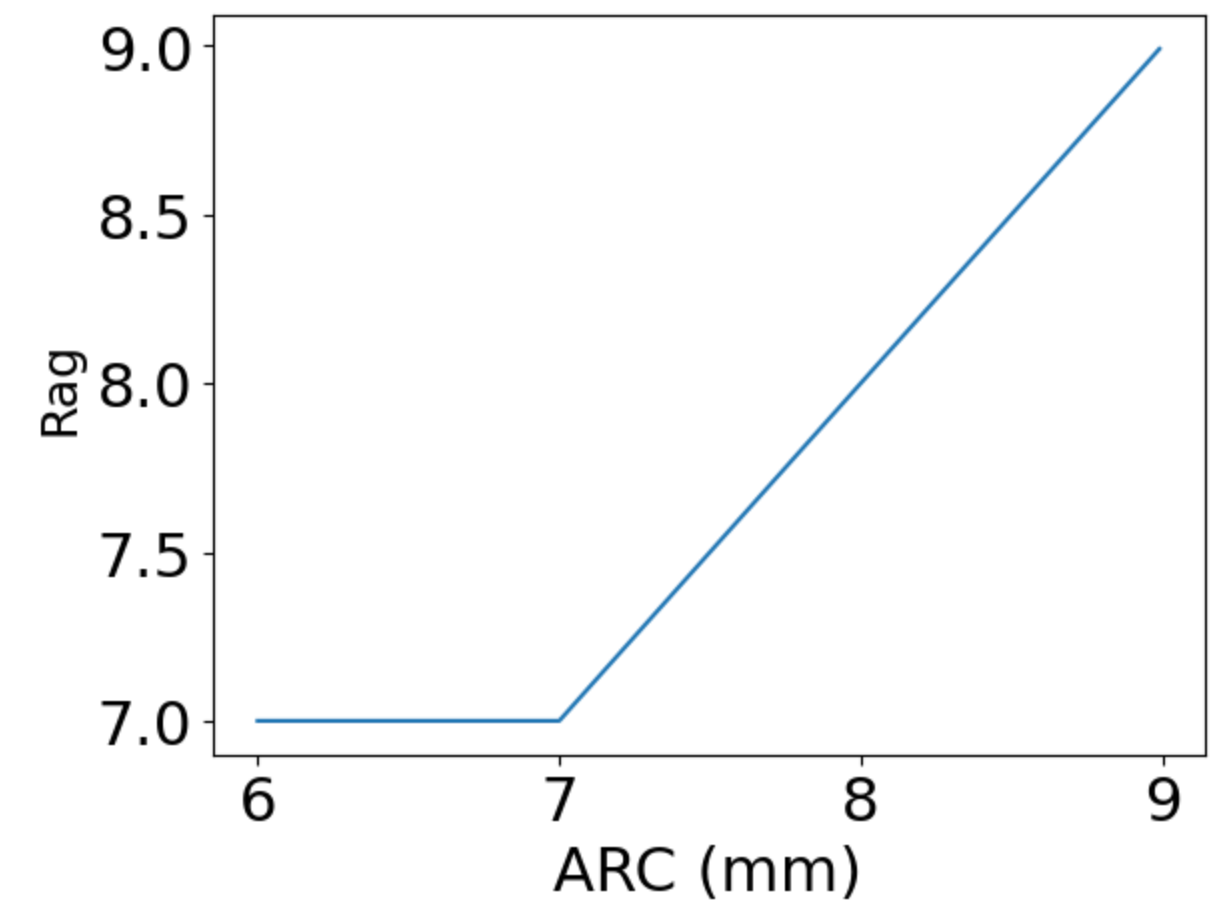
Rag is equal to R, floored at 7 mm. 
def setAG(LA): 
    AG = 12.5 * LA / 23.45 
    if AG > 13.5: 
    	AG = 13.5 
    else: 
        AG = AG 
    return AG
    
# the AG has a ceiling when greater than 13.5 : this corresponds to an AL value of 25.32mm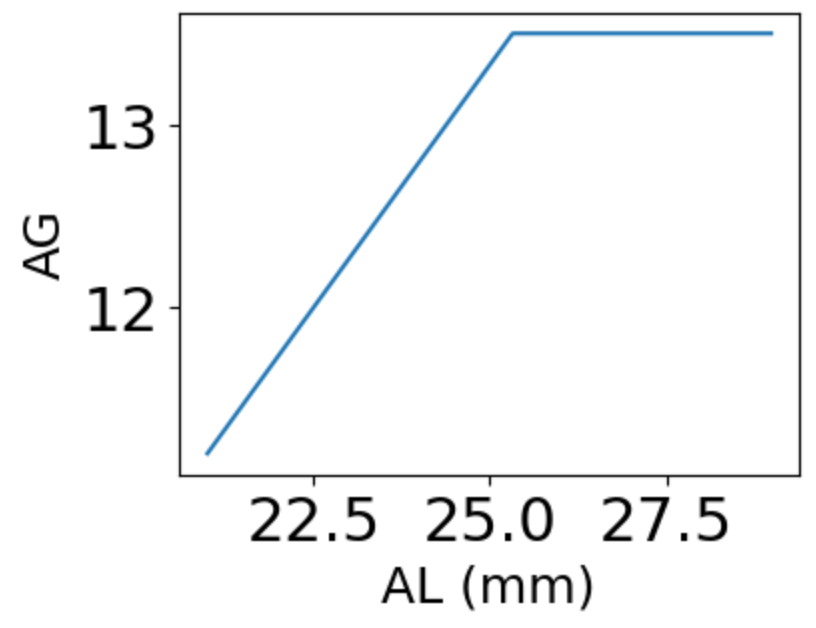
AG is a function of AL, with a ceiling at 13.5

The lens position, ACD, is a function of Rag and AG : 

def setACD(Rag, AG): 
    ACD = 0.56 + Rag - (math.sqrt( (Rag**2) -((AG**2) /4) )) 
    return ACD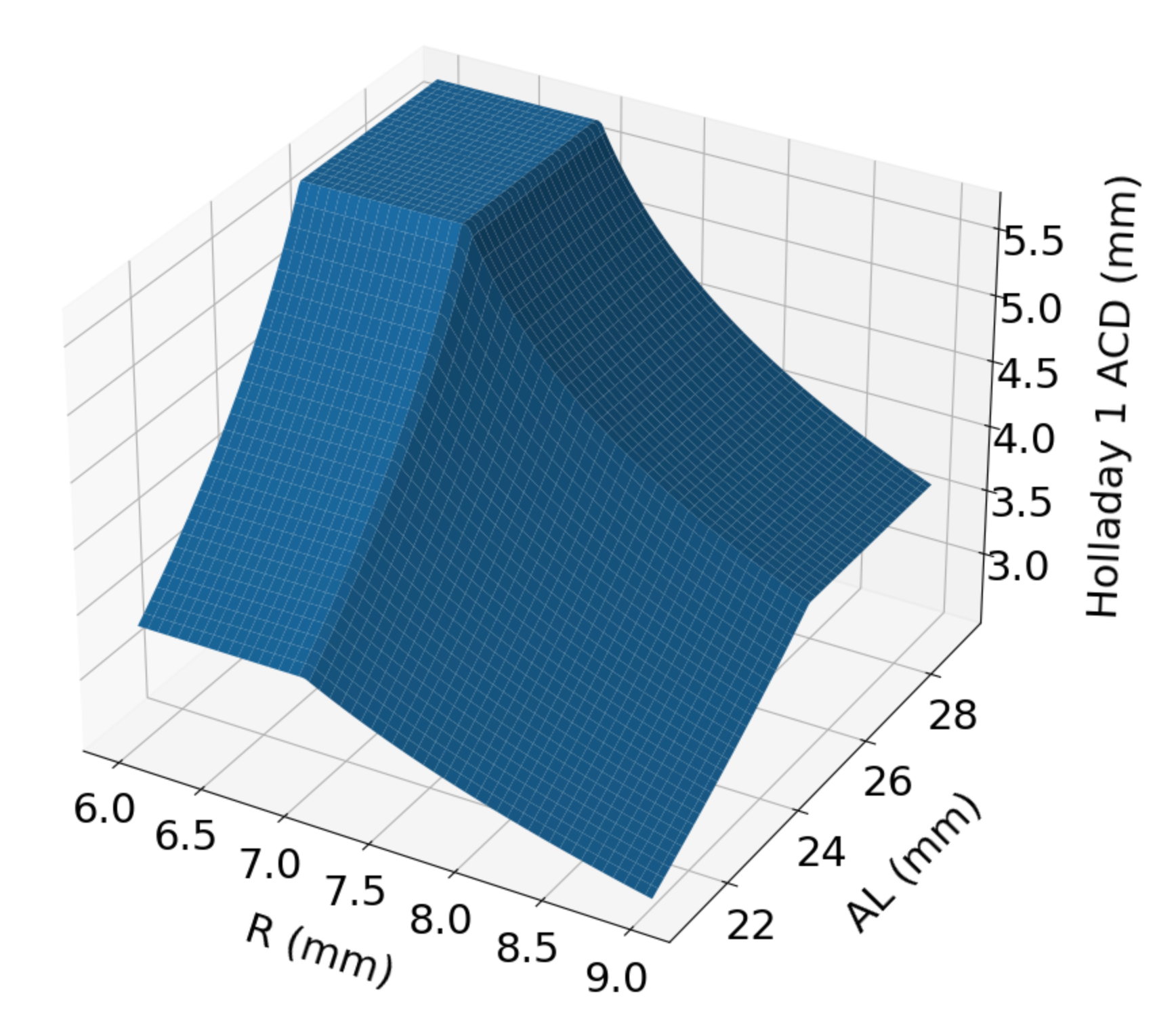

A retinal thickness value of 0.2mm is added to the AL.

Final Holladay 1 function : 

def Holladay_SE(LA, R, SF, power): 
    Rag = setRag(R) 
    AG = setAG(LA) 
    ACD = setACD(Rag, AG) 
    nc = 4/3 
    na = 1.336 
    RT = 0.2
    V = 12 
    ALm = LA + RT 
    num = 1000*na*(na*R - (nc - 1)*ALm) - power*(ALm - ACD - SF)*(na*R - (nc - 1)*(ACD + SF)) denum = na*(V*(na*R-(nc-1)*ALm)+ALm*R)-0.001*power*(ALm-ACD-SF)*(V*(na*R-(nc-1)*(ACD+SF))+(ACD+SF)*R) result = round(num / denum, 3) 
    return result

The Haigis Formula

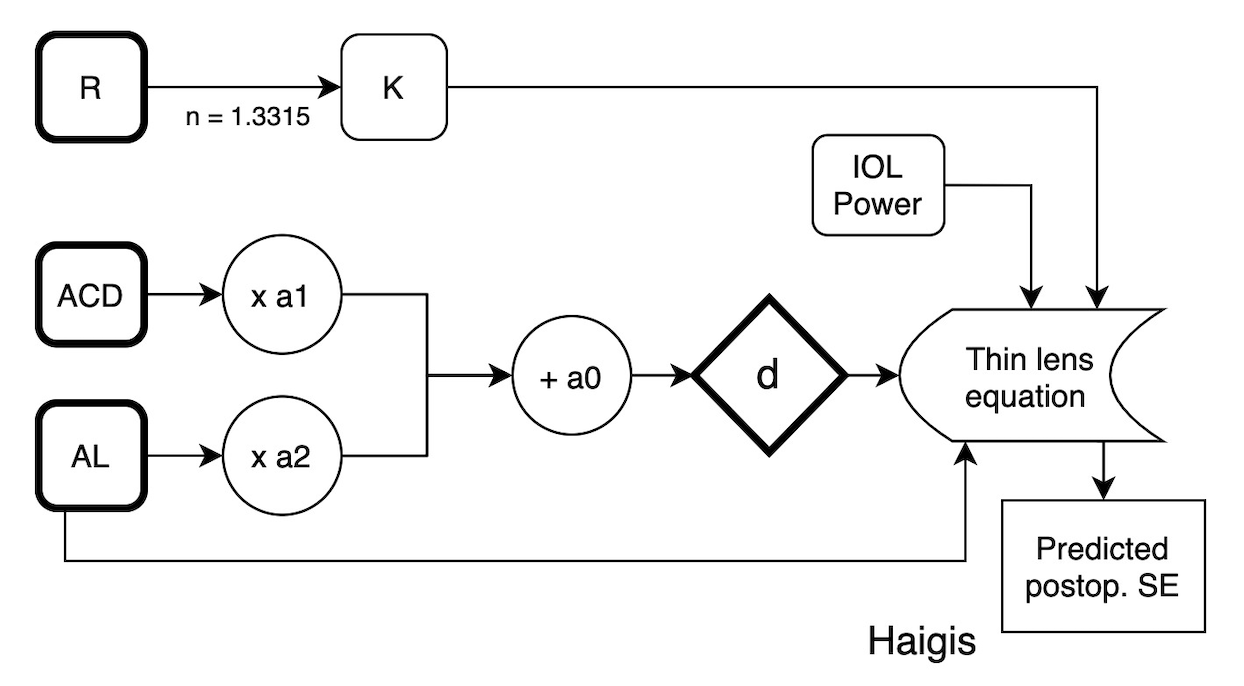
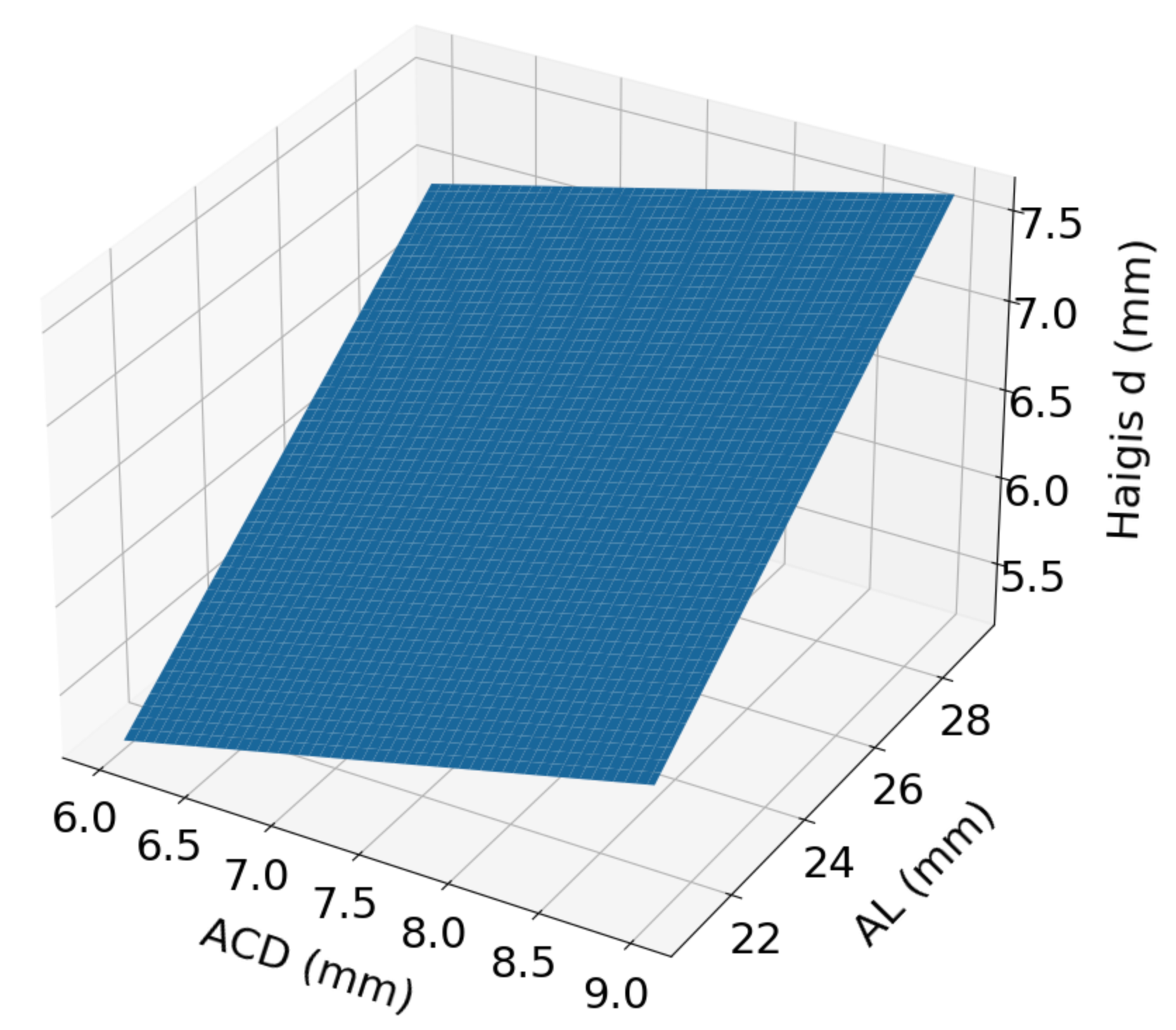
The Haigis formula (9) is the most simple third generation formula... and also consistently has the best outcomes when using its triple-optimized version. The lens position d is obtained using a multiple regression taking ACD and AL as inputs :

d = a0 + a1 x ACD + a2 x AL

The Haigis formula is beautifully simple. The lens position value (d) is a function of ACD and AL, using simple coefficients (a1 and a2, respectively) and a constant (a0). K is calculated from R using a keratometric index of 1.3315. Neither AL or K are transformed before being used in the optical equation.

What's your favourite approach ?

References

1. Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg. 1990 May;16(3):333-40.

2. Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula: Erratum. J Cataract Refract Surg. 1990;16(4):528.

3. Haigis W. Occurrence of erroneous anterior chamber depth in the SRK/T formula. J Cataract Refract Surg. 1993 May;19(3):442-6.

4. Hoffer, Kenneth J. M.D.a. The Hoffer Q formula: A comparison of theoretic and regression formulas. Journal of Cataract & Refractive Surgery: November 1993 - Volume 19 - Issue 6 - p 700-712

5. Hoffer, Kenneth J. MD. Reply: Errata in printed Hoffer Q formula. Journal of Cataract & Refractive Surgery: January 2007 - Volume 33 - Issue 1 - p 2-3
doi: 10.1016/j.jcrs.2006.08.056

6. Zuberbuhler B, Morrell AJ. Errata in printed Hoffer Q formula. J Cataract Refract Surg. 2007 Jan;33(1):2; author reply 2-3.

7. Hoffer, K. Errors in self-programming the Hoffer Q formula. Eye21, 429 (2007).

8. Holladay JT, Musgrove KH, Prager TC, Lewis JW, Chandler TY, Ruiz RS. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg. 1988;14(1):17–24.

9. Haigis W, Lege B, Miller N, Schneider B. Comparison of immersion ultrasound biometry and partial coherence interferometry for intraocular lens calculation according to Haigis. Graefes Arch Clin Exp Ophthalmol. 2000;238(9): 765–773.